This brief explanation describes the methods used in the simulation above to determine the Right Ascension (RA) and Declination (Dec) of the Sun, Mercury, Venus, Mars, Jupiter, and Saturn. It assumes some background in astronomy. However, there is a reasonably verbose glossary linked to what may be unfamiliar terms. In truth, this explanation is more for those wishing to know exactly what assumptions underlie the above simulation. However, this explanation does serve as a good case study in how to determine the planets' positions.
The simulation overlays the RA and Dec of the five planets visible to the naked eye and the sun atop an cylindrical projection of the Earth's sky. The name planet roughly translates to "wanderer." Knowing the geocentric model held for so long, many of my students simply assume the planets move about the sky in much the same manner as the moon or sun--steadily creeping eastward. They do not, and I developed this simulation to illustrate their true wandering nature.
Solving Kepler's Equation & Calculating Ephemerides
When first approaching this problem, I knew that I would need to solve Kepler's Equation and have a little fun with reference frames. I was surprised by the explanations available on the web. Most of them fell short of what I was looking for. They were either strictly qualitative or, if quantitative, unnecessarily opaque. This resulted mostly from having too few or poorly executed diagrams and illustrations. There were a few notable exceptions, and I have cited them in the references section. As I never formally studied celestial mechanics, these sources were my teachers and greatly helped acquaint me with the problem and its solutions. What I've attempted to do here is to weave together a relatively cogent "How to" on the solving of Kepler's Equation and the calculation of planetary positions in the Earth's sky.
Johannes Kepler (1571-1630) was a mathematician, astronomer, and Copernican. He believed that the Sun, not the Earth, lay at the center of the universe. He refined Copernicus's view of a heliocentric (Sun-centered) universe, making it into more than simply a competing theory for the geocentric (Earth-centered) model. Under Kepler it would become the superior predictive model. In his work Kepler formulated three laws of planetary motion first set down together in Harmonice Mundi (Harmonies of the World), 1618, and here they are.
-
Kepler's Laws:
1. The planets orbit about the Sun in elliptical orbits with the sun centered at one of the ellipse's two foci (Figure 1).
2. An imaginary line connecting the sun and a planet sweeps out equal areas in equal times as the planet moves through its orbit. A consequence of this is that a planet moves fastest when closest to the Sun. Newton will have something to say about this.
3. The square of the period of a planet's orbit is proportional to its distance from the Sun cubed. When the units used for distance are Astronomical Units (AU) and time is measured in years, this relationship can be written explicitly as an equation relating the planet's period P and the semi-major axis of its orbit a (eq.1).
Kepler's Laws meant that given only a handful of orbital parameters, one could say where a planet had been and would be. To state this explicitly, astronomers make use of Kepler's Equation (eq.2).
Kepler's equation is a transcendental equation. This means there is no general solution. So to find the location of a planet at a time t, we must solve for that time using some numerical method. First let us work with what we have. NOTE: You may find it helpful to reference Figure 2 (pop-up) to help visualize some of the variables referenced here.
Only e is time independent. So we consult our orbital parameters for its value and then solve for the mean anomaly (eq.3), M in Kepler's Equation (eq.2). The mean anomaly is just the angle with the perihelion that the planet would have if the orbit was an ellipse with eccentricity = 0, i.e., a circle. We call the imaginary planet moving along such an orbit the mean planet. In such a case the planet would move with a velocity V = (2*PI)/Period .
As you can see, the mean anomaly is just the mean planet's velocity times the time elapsed since it was last at the perihelion.
We can now find the eccentric anomaly using some numerical method. This simulation makes use of successive approximation. Once we have a value for E with which we are happy, we can find the true anomaly (eq.4). The true anomaly is the ACTUAL angle between the perihelion and the planet.
From here it is a simple matter to find the planet's radial distance (eq.5) from the sun.
We now have the planet's polar coordinates (r, v) within the plane of its orbit such that the X axis points from the Sun towards the Perihelion, point P.
Now we find the Heliocentric Ecliptic coordinates (x, y, z) for the planet by converting from polar to cartesian coordinates and rotating the frame such that the X axis points towards the first point of Aries.
We then rotate the coordinates into Heliocentric Equatorial coordinates (X, Y, Z), making use the matrix below.
However, our display shows the positions of the planets from the Earth. So we need to switch our vantage point to that of a geocentric system. To do this we first repeat the above process, solving for the Earth's Heliocentric Equatorial coordinates. We want to know the Sun's Geocentric coordinates. So here we will approximate this as the inverse of Earth's heliocentric coordinates. This is the same method used to find the Sun's location for display. It is important to note, however, that this is just an approximation, as what we really find is not the location of the Earth but rather that of the Earth-Moon system's barycenter. This simplification is responsible for limiting the simulation's accuracy. Note: This is not an issue for the Build Your Own Solar System simulation for teachers as the hypothetical "Earth" has no moon in that simulation. We then add the Sun's geocentric coordinates to those of the heliocentric coordinates of our planet. This shifts the coordinates, giving us the Geocentric equatorial coordinates (xp, yp, zp) for the planet.
Having the planet's Geocentric coordinates, it is a simple matter to convert them into Right Ascension and Declination. Note: Watch you signs here; if you're not careful, it WILL get messy.
That's it. We can now solve for many discreet times and collect the data into tables to construct ephemerides. If you are interested in finding more accurate calculations for the planets' positions, consider buying a copy of the Astronomical Almanac from the US Naval Observatory or making use of JPL's Horizons system.
References & Further Reading:
1. To anyone interested in why it is the orbits of the planets are elliptical, I suggest finding a copy of D. & J. Goodstein's Feynman's Lost Lecture: The Motion of Planets Around the Sun. W. W. Norton & Company. New York, NY. 1996.
2. A copy of Kepler's Harmonice Mundi (Harmonies of the World) as well as many other ground breaking texts in astronomy have been compiled into one tome: Stephen Hawking's On The Shoulders of Giants: The Great Works of Physics and Astronomy.
3. For what I found to be the most rigorous on-line handling of this material, try Dr. J. B. Tatum's Celestial Mechanics: http://orca.phys.uvic.ca/~tatum/celmechs.html (Link current as of April 2004).
4. The orbital parameters used here came from the JPL Solar System Dynamics Group's "Planetary Orbital Elements," JPL Solar System Dynamics: http://ssd.jpl.nasa.gov/elem_planets.html. (Link current as of April 2004).
Ascending node: The point of intersection between a planet's orbit and the plane of the Sun's equator, where the planet is moving northward ("upward") across the plane of the Sun's equator.
Astronomical Units (AU): A measure of distance where one AU is just about equal to the average distance of the Earth from the Sun, 1.49597870691 x 108 (± 3) kilometers.
Celestial equator: The projection of the Earth's equator onto the celestial sphere.
Descending node: The point of intersection between a planet's orbit and the plane of the Sun's equator, where the planet is moving southward ("downward") across the plane of the Sun's equator.
Above are four ellipses with varying eccentricities. The first is a circle.
Ecliptic: As seen from the Earth the ecliptic is the Sun's annual path across the sky.
Elliptical: Shaped like an ellipse.
Foci: Plural of focus. See ellipse.
Orbital parameters: A set of physical parameters for the orbit of a planet sufficient to predict the position of the planet at a given time t. The orbital parameters used in the simulation above can be found at: http://ssd.jpl.nasa.gov/elem_planets.html (valid as of June 2004).
Perihelion: The closest point on a planet's orbit to the Sun.
Period (of a planet): The length of time it takes a planet to return to the same place in its orbit.
PI (
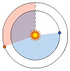
Retrograde Motion: The westward motion of the planets against the background stars. In order to maintain the Earth's central location and a commitment to perfect circular motion, geocentrists devised a set of epicycles (orbits within orbits) upon which the planets would rotate. The motion of the planet about its epicycle allowed for the presence of retrograde motion. However, heliocentrists' Sun-centered model had no need for epicycles as retrograde motion could bee seen as one planet simply overtaking another as they raced about the Sun. See Animation.
Sidereal period: A planet's sidereal period is what many often think of as the planet's year--the time it takes to make one full revolution about its orbit. See Animation.
Synodic Period: A planet's synodic period id the time between two identical configurations in the sky as seen from Earth (e.g., the time between two oppositions). See Animation.
True Anomaly: The angle between the perihelion and the planet as measured in the plane of its orbit.
Vector: A quantity consisting of both direction and magnitude (e.g., velocity).
Velocity: A measure of an object's motion that includes both the object's speed and direction.
A free tool for creating and observing your own solar system, designed for astronomy teachers & students.
A dynamic illustration (animation) of retrograde motion, portraying the geocentric and heliocentric models.
A dynamic illustration (animation) of a planet's synodic & sidereal period.
An app that helps solve common introductory mechanics problems, consider it training wheels for learning mechanics.
Answers to science questions, brief lessons, and ideas for teachers and students.
An on-line tool and database for running quiz bowl practice rounds in accordance with National Science Bowl rules.
Phylm, pronounced "film," is a portmanteau combining physics and film and the umbrella name given to a number of physics/film projects I've worked on, including an annual Phylm Prize, and a curricular unit for physics teachers.
My first byline, Moving Targets is a Hot Science piece I wrote while interning for NOVA Online, the companion site to PBS's NOVA. It explains how to measure the radial velocities of stars.